Building Intuition for Random Forests

Random Forest — A group of decision trees — is a powerful machine learning algorithm
It is intriguing to see how simply and easily a random forest can yield extremely useful results. Random Forest is a supervised machine learning algorithm.
Random Forests are essentially an ensemble of decision trees. In its simplest form a Decision tree is a sequence of choices.
As far as accuracies of prediction go Decision Trees are quite inaccurate. Even one mis-step in the choice of the next node, can lead you to a completely different end. Choosing the right branch instead of the left could lead you to the furthest end of the tree. You would be off by a huge margin!

A huge number of decision trees created randomly using input data comprise the Random Forest. The randomness of creation combined with simplicity of a Decision Tree lends Random Forests their awesomness!
Random Forests = Simplicity of DT + Accuracy Through Randomness
Random forests (Breiman, 2001) were originally conceived as a method of combining several CART (Classification And Regression Trees) (Breiman et al.,1984) style decision trees using bagging (Breiman, 1996). In the years since their introduction, random forests have grown from a single algorithm to an entire framework of models (Criminisi et al., 2011), and have been applied to great effect in a wide variety of fields — Computer Vision, Medical Image Analysis, Drug Discovery, Chemoinformatics etc.
Without going into further praise of Random Forests let’s see how to deal with them
- How to build a random forest?
- Why does it work?
1) Building a Random Forest
There are 3 steps involved in building a random forest.
- Create a ‘bootstrapped dataset’ from the original data.
- Create a decision tree using this bootstrapped data.
- Repeat 1 and 2 to create more decision trees.
Step 1 — Bootstrapping /Bagging — To begin building a random forest we need to first create “bootstrapped datasets” from our original dataset. Bootstrapping is a technique to pick up samples randomly from our dataset. In doing so we are allowed to pick up the same sample twice. In Statistical Jargon it’s known as Sampling with replacement.
Rule of thumb —Generally if there are S number of trees in the Random Forest we create S Bootstrapped Datasets.

Example
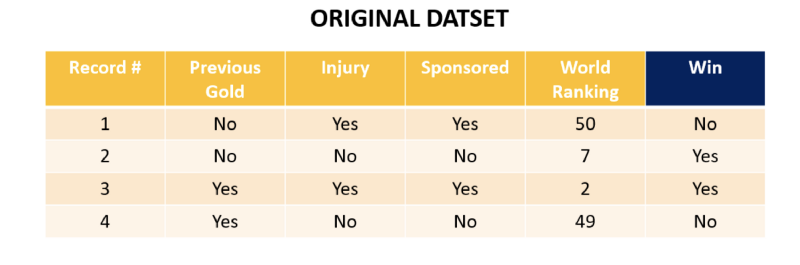
Let’s say we have Olympics 2020 coming up. Our Random Forest has to predict whether a player will win a medal this year or not. It takes the following 4 variables into account
- Has the player won Gold Medal previously?
- Has the player had any recent injury?
- Is there sponsorship available for the player?
- Player’s current world rank.
Also, for example’s sake let’s consider our dataset has only 4 players. Each row is a record/datapoint. So we already know that player with the ranks 49 and 50 player are predicted to not win any medals. Just the players with rank 2 and 7 are predicted to win.
Now let’s create the bootstrapped dataset as step 1 of understanding what Random Forests are!
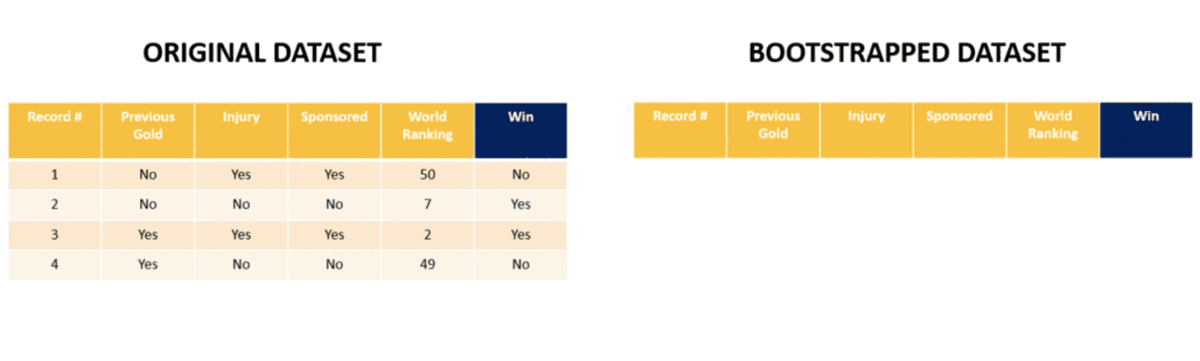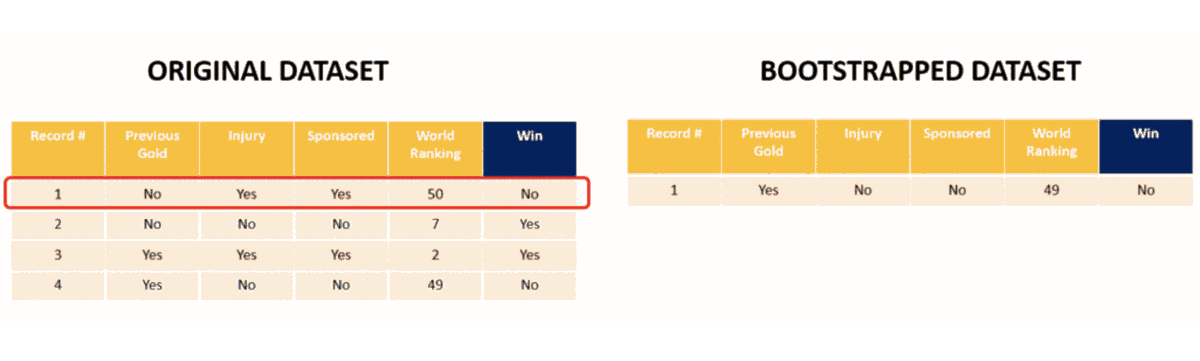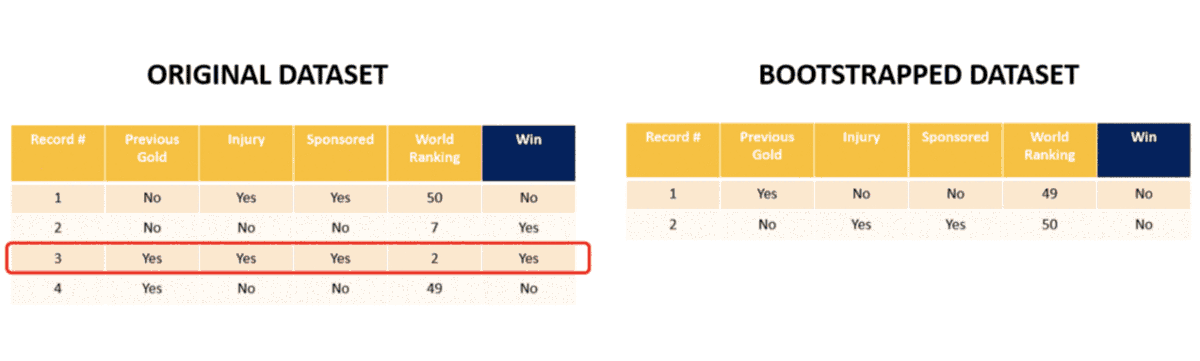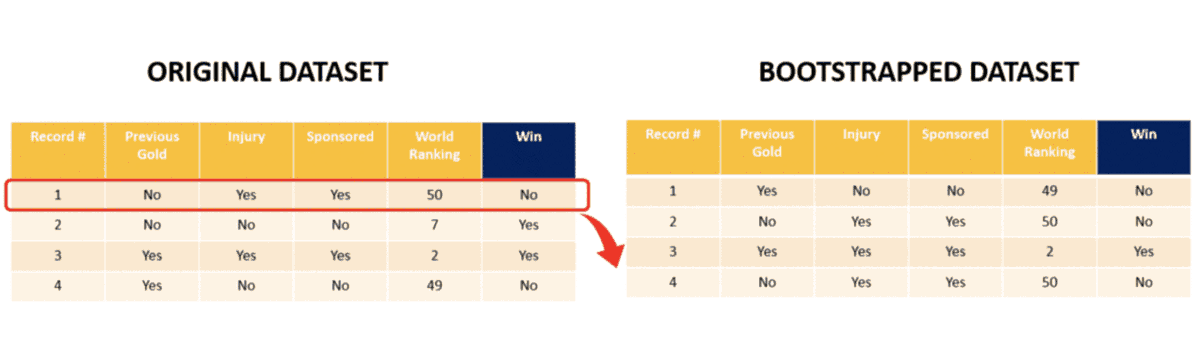
Let’s begin by choosing one row from the above table randomly. Let’s say we end up picking row 4. It goes as row no. 1 in the ‘bootstrapped dataset’. Next we pick row 1 from the original table. Note that bootstrapped dataset has the same number of datapoints/rows as the original dataset. 2 more samples later we have our bootstrapped dataset. Note that row 1 is picked twice randomly (it goes as row 2 and 4 in the bootstrapped table) and row 2 is never picked!!
Step 2 — Create a Decision Tree — Once we have a bootstrapped dataset we create a decision tree from it. Remember the most important thing while creating a decision tree is to know which is the best question to ask. As explained in the Decision Tree article Gini Impurity gives a measure of which question separates the data best.
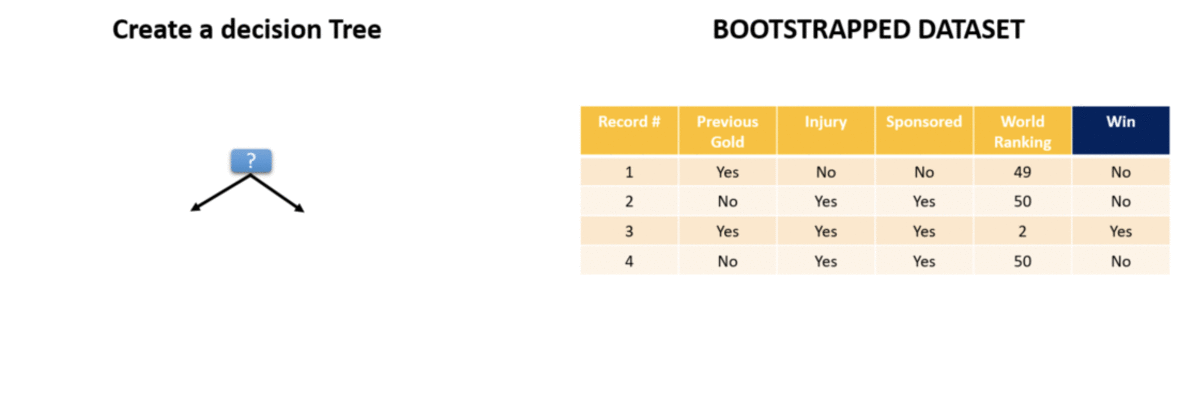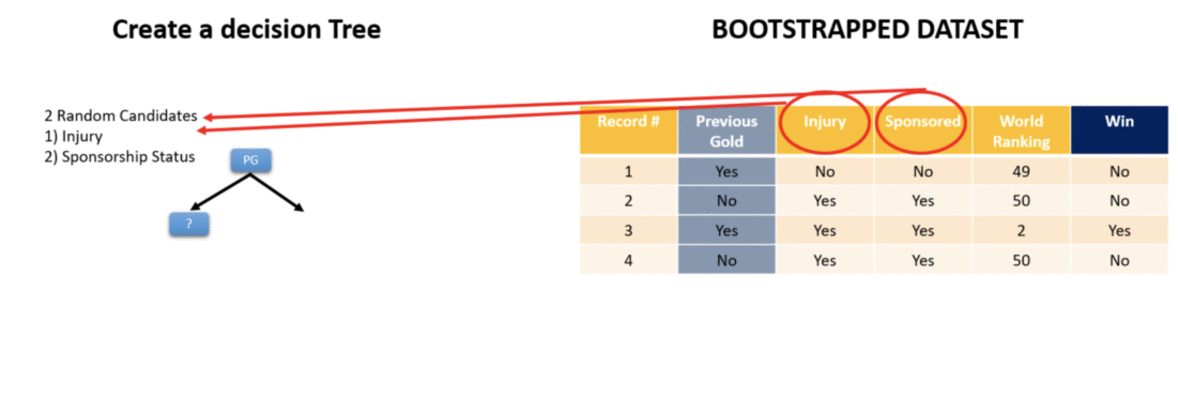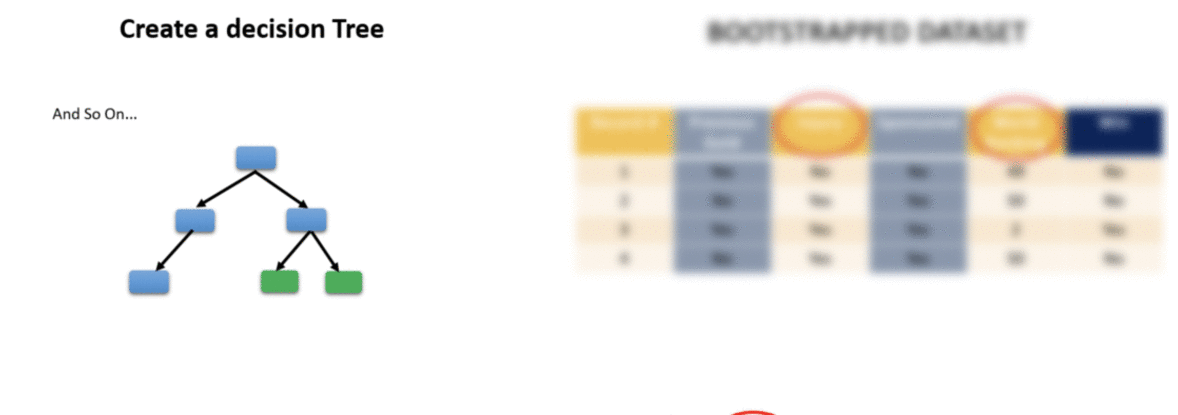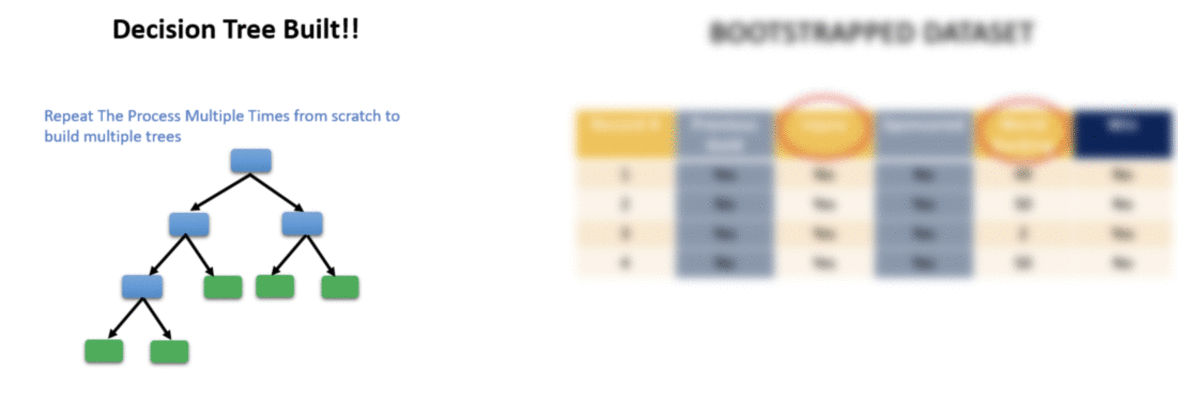
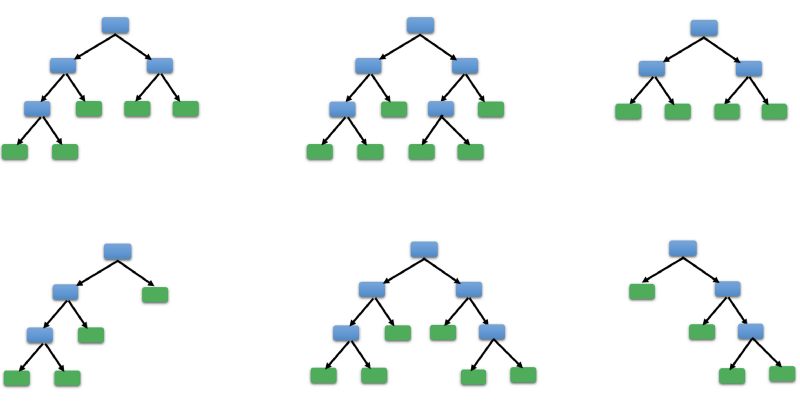
Step 3 — Rinse and Repeat — Once you have 1 decision tree start the whole iteration all over again. Create a new bootstrapped dataset and considering only a subset of variables at each step you can come up with a wide variety of Decision Trees. Ideally you would need 100s of trees but for representation purpose we just show 6 trees below. Note each tree comes from a different bootstrapped dataset.

This randomness in the tree creation process is what lends flexibility and high accuracy to Random Forest
2) Why does it work?
It works because of different perspectives given by each tree. Consider a company that is hiring for the position of CTO. A few people are assigned the role of interviewing the candidates, according to their own strengths.
- CEO — Judges the leadership qualities
- Tech. Director — Judges the technological awareness
- HR Director — Judges the personality and cultural fit
- Board Members — Judge the managerial qualities
- A few star employees — Judge depth of knowledge in specific segments
Each of these interviewers have their own strengths that they have acquired over many years of experience. But these strengths also become biases! Each interviewer is poised to choose a candidate who’s strong in their own expertise area.
If it were upto just the Star Employees they would end up hiring a CTO who works great as an independent contributor but might not a be a visionary leader (which was CEOs role to judge).
Random Forest works similarly. Each tree is an interviewer. Each tree is biased to give results favouring a particular variable. Their combined results although come out to be pretty accurate. The whole company is the Random Forest and churns out more accurate results than an average employee a.k.a Decision Tree
Random Forest at work
Going with the example Dataset used before. Let’s say a new player registers for the race. His variables are as follows:
- Previous Gold Winner : No
- Any Recent Injury : No
- Sponsorship Available : No
- World Ranking : 7
The question is Will the player win a medal in this race?
Let’s see how and what does the Random Forest predict?

The process given above is called Bagging
Bootstrapping the data & using an aggregate of ‘individual results’ to obtain the ‘final result’ is called Bagging
That’s about it. What remains is testing how well our forest works. Stay tuned for a future article on the same.
Member discussion