Layman’s Introduction to Linear Regression
When your data follows a straight line trend, linear regression is your friend
Linear regression attempts to model the relationship between two variables by fitting a linear equation (= a straight line) to the observed data. One variable is considered to be an explanatory variable (e.g. your income), and the other is considered to be a dependent variable (e.g. your expenses).
What linear regression does is simply tell us the value of the dependent variable for an arbitrary independent/explanatory variable. e.g. Twitter revenues based on number of Twitter users .
From a machine learning context, it is the simplest model one can try out on your data. If you have a hunch that the data follows a straight line trend, linear regression can give you quick and reasonably accurate results.
Simple predictions are all cases of linear regression. We first observe the trend and then predict based on the trend e.g. How hard you must brake depending on the distance of the car ahead of you. Not all of situations follow a linear trend though. e.g. the rise of bitcoin from 2015 to 2016 was linear but in 2017 it suddenly became exponential. So post 2017 Bitcoin would not be predicted well by linear regression
Hence it is important to understand that even though linear regression can be the first attempt at understanding the data it may not always be ideal.
Here’s how we do linear regression
- We plot our dependent variable (y-axis) against the independent variable (x-axis)
- We try to plot a straight line and measure correlation
- We keep changing the direction of our straight line until we get the best correlation
- We extrapolate from this line to find new values on y-axis
Extrapolation is to ‘Make a Prediction’ based on ‘some information’
This is essential to differentiate Linear Regression as a statistical technique from it as a machine learning algorithm. ML is more concerned with the predictions, and statistics is more concerned with the parameter inference
Terminology-wise‘prediction’ = dependent variable and
‘some information’ = independent variables.
Linear Regression provides you with a straight line that lets you infer the dependent variables
Example — Beer Control
Linear regression at its core is a method to find values for parameters that represent a line.
The equation Y=mX+C
In terms of coordinate geometry if dependent variable is called Y and independent variable is called X then a straight line can be represented as Y = m*X+c. Where m and c are two numbers that linear regression tries to figure out to estimate that white line.
Look at the figure below. Let’s say you decide to become conscious of how much you drink.
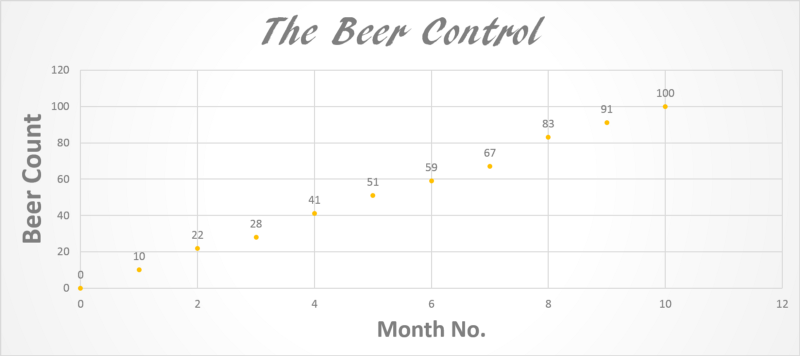
What do you see? How many beers roughly do you drink each month? A simple look shows you drink roughly 9-10 pints per month (Not bad!).
What do you expect the trendline to look like? How many beers at the end of the year?
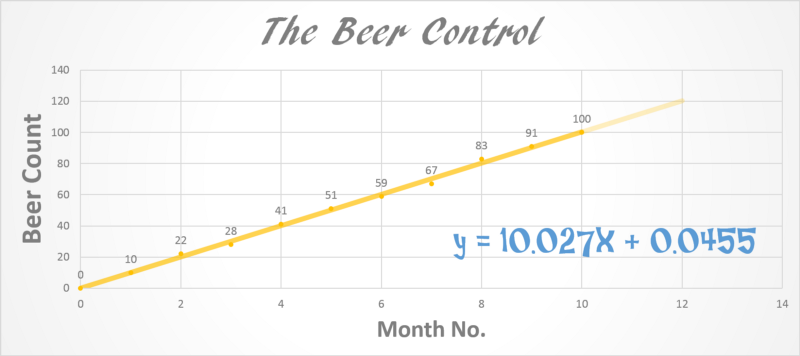
A simple linear regression shows what we could clearly see.
Y = 10.027X + 0.0455 => m=10.027, c = 0.0455
c is a very small number so for now we will ignore it. Look at that the line equation tells us that for every month we drink 10.027 beers. That’s the trend. I derived this equation in MS PowerPoint but how can we do this mathematically?
How do machine learning engineers do this?
General Equation for Linear Regression
Bear with me. There is a slight bit of mathematics in this section but we will breeze right through it.
Linear regression is a form of supervised learning. Supervised learning involves those set of problems where we use existing data to train our machine. In the beer example we already know the data for the first 10 months. We just have to predict the data for 11th and 12th month.
Linear regression can involve multiple independent variables. e.g. house price (dependent) depending on both location (independent) and land area (independent) but in its simplest form it involves 1 independent variable.
In its generic form it is written as
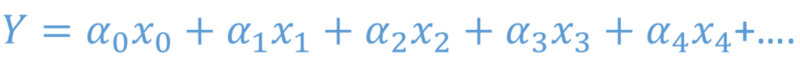
where all the alphas are coefficients that our machine learning algorithm has to figure out. The x’s are known because they are independent. We can set them anything. What we need to find is Y.
For a single independent variable the equation is reduced to
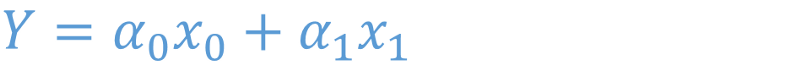
For simplification x0 is set to be equal to 1 and alpha0 is given the name c. x1 is called x and alpha1 = m. It reduces to:
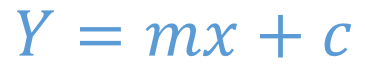
Jargon
To figure out m and c we draw a line, using an initial guess of m and c through the set of points that we already have. We calculate the distance of this line from each of these points. We take square-root of the sum of the squares of these distances (Cost Function) . We keep changing m and c in small steps to see if this Cost Function decreases. When the cost stops decreasing we fix that m and c as our final result. The resulting line is our best linear fit through the data. Now for any new x we can figure out the y using this line.
What this jargon means is that we keep redrawing the line until it seems to fit the data best. That’s all the jargon that was needed.
Machine Learning
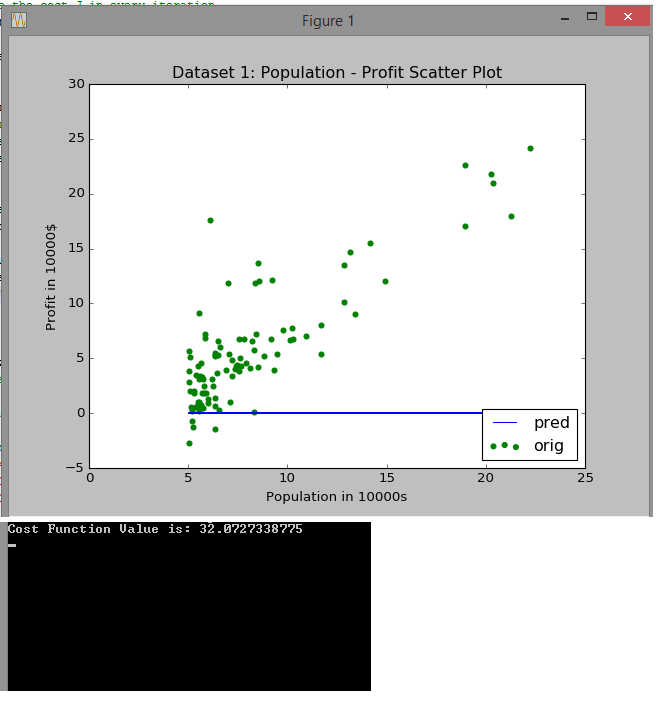
Below we have a dataset of population vs profit. We draw a scatter plot and try to fit a straight line through it. Look closely at how the initial guess (blue line) shifts towards the trend that the data follows. Also look at how many iterations are needed to reach that stable cost of 5.87
It starts with a cost of 32 and an initial guess way off!
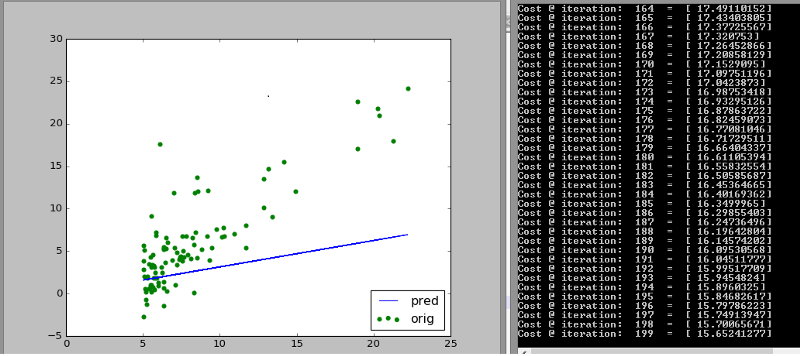
It steadily improves from then on. After 200 iterations the cost has already halved.
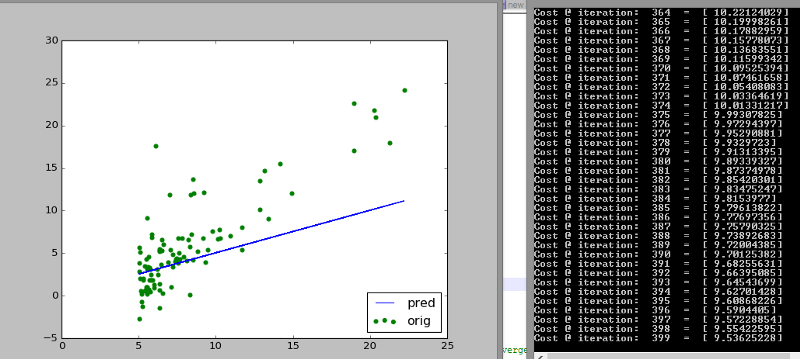
After 400 iterations the cost is 1/3rd
The guess improves further at 600 iterations
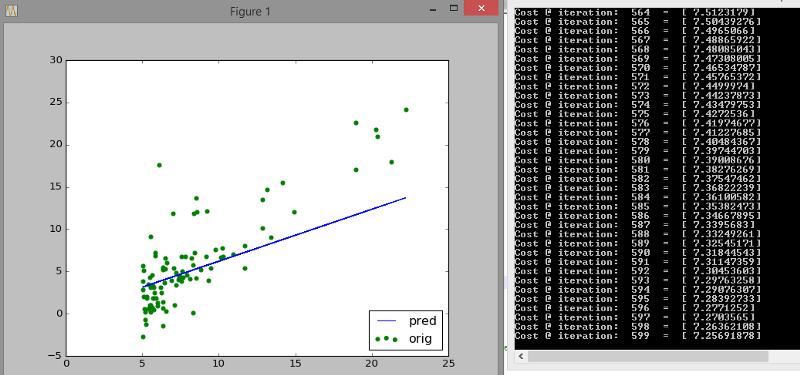
After a 1000 iterations the decrease in cost has slowed down and the fit is more or less stable
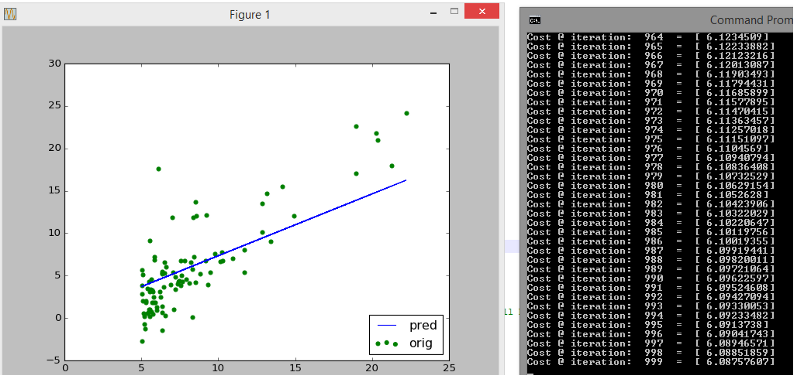
After 3000 iterations we are confident that we have a good fit

It is as simple as that! What is clear is that linear regression is a simple approach to predict based on a data that follows a linear trend. It follows that we will fail rather drastically if we were to fit a sine curve or a circular data set.
Finally, linear regression is always a good first step (if the data is visually linear) for a beginner. It is definitely a good first learning objective!
Member discussion