Understanding ML Evaluation Metrics — Precision & Recall

The jargon of machine learning world is crucial to convey how well your model works

Touching base, quoting a ball park number, hitting it out of the park, it being a whole new ball game are all examples of the jargon that is borrowed from the world of baseball and heavily used (or misused in some cases) in the corporate world.

Machine learning world similarly uses a set of terms routinely, to specify how well the models are working. The question arises — why do we need anything other than the term accuracy? Accuracy is simply defined as

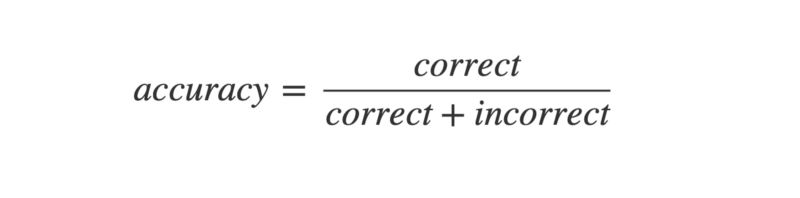
Now imagine that an oncologist, an expert in breast cancer, has 1000 patients. He decides to declare all his patients as free of cancer but then later on finds out that 3 of those actually did have cancer. For the doctor it still means an accuracy of 99.7% but for those 3 patients the results are very severe. This thus is the pitfall to using just accuracy as your success metric.

These kind of “naive” results are obtained when we encounter an imbalanced dataset. An imbalanced dataset is one which has too few examples of one kind.

Use of precision & recall in the real world

Precision, recall, sensitivity and specificity are terms that help us recognise this naive behaviour. Routinely the ML teams in companies like Microsoft, Amazon ask their employees to quote the PR (precision and recall) numbers or to quote the sensitivity and the specificity of the results.

These numbers help us understand what is relevant in the data

Let’s understand with an example. Let’s say our oncologist treats 1000 patients.

• He declares 950 of them to be free of cancer. In doing so he makes 10 mistakes. 940 of these he correctly diagnoses to be free of cancer. The unfortunate 10 have cancer but escape doctor’s notice.
• He diagnoses the remaining 50 to have cancer. Of these only 5 patients really have cancer. Rest of the 45 patients are free of cancer but have been incorrectly identified as cancer patients.

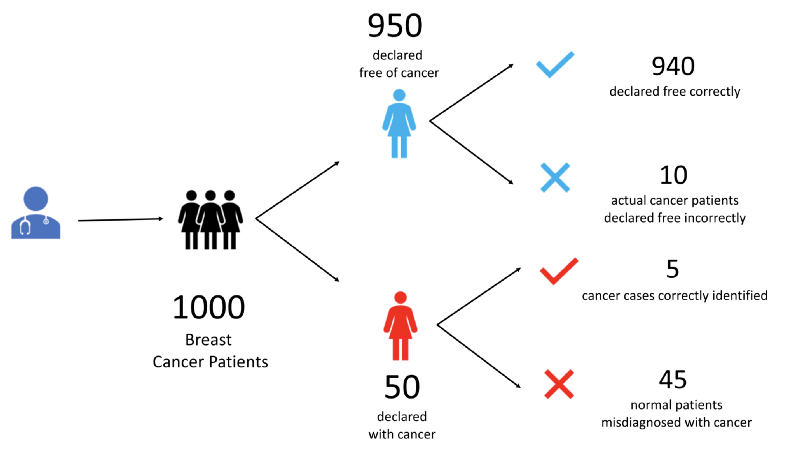
At the end we have 4 set of patients. Let us label all these 4 kinds of patients.

• True Positives (TP) —5 patients who are tested positive for cancer correctly
• False Positives (FP) —45 healthy patients that are tested positive incorrectly
• True Negatives (TN) — 940 healthy patients who tested negative for cancer correctly
• False Negatives (FN) — 10 patients who had cancer but were declared negative for cancer incorrectly

The word positive means a ‘yes’ to a question we are asking. e.g. Does this person have cancer? A positive would be when we say ‘yes this person has cancer’. A negative would then mean when we say that, ‘this person does not have cancer’.

Let’s look at these 4 terms pictorially

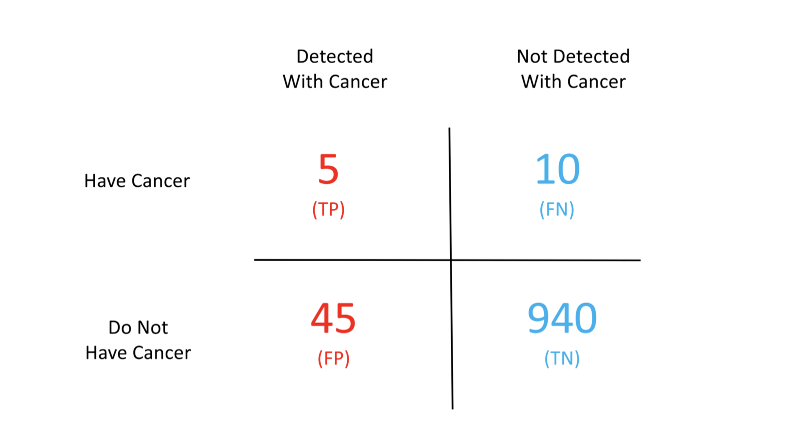
The above chart is popularly known as the confusion matrix. Confused eh? Don’t be. This matrix becomes the solution to our problems. Given this matrix we can easily compute all of the terms we have been talking about so far.

First let’s look at how accurate the doctor has been. The number of correct decisions that the doctor has taken are the ones labelled true.

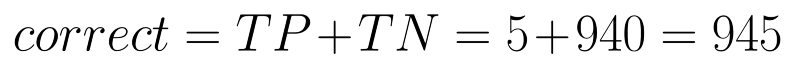
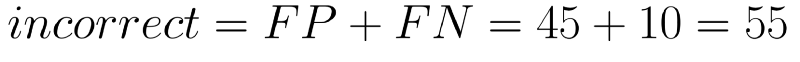
Given these numbers our accuracy comes out to be 94.5%

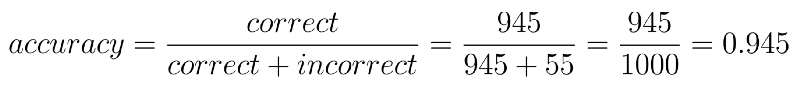
Even though this seems like a high number it still leaves out a lot of patients susceptible to extreme losses. Take for example the False Negative (FN) patients. These 10 people would be relieved that the doctor has given them a clean chit whereas the cancer would be causing harm in the meanwhile.

This is where the above terminology comes to our rescue.

Precision tells us how relevant are the positive detections. Higher the precision better is our detection mechanism. e.g. in our example precision is just 10% which is very poor. We are misclassifying a lot of healthy patients as cancer patients.

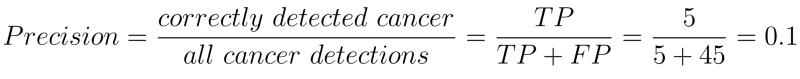
Precision is just part of the picture. Another way to look at our data is through recall. Recall is the same as sensitivity.

They tell us what percentage of actual positives are detected. i.e. what percentage of real cancer patients are detected. It is computed by taking the ratio of correctly identified cancer patients (true positives) to the total number of cancer patients (true positives + false negatives).

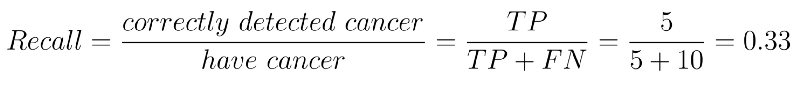
This means we are only able to detect 33% of the total cancer patients correctly. That is bad!

Specifity tells us how good the system is at removing false alarms. It is computed by taking the ratio of patients who are correctly detected to not have cancer (true negatives) to all the patients who do not have cancer (true negatives + false positives).

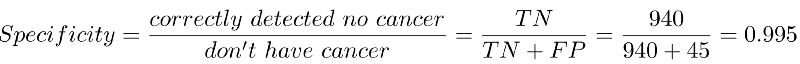
We are able to weed out false positives 99.5% of the times. That’s very good.

So what do these numbers tell us?

1. High Precision + High Recall — The prediction model (i.e. the doctor in our case) is highly dependable. The model doesn't misclassify healthy patients and doesn’t wrongly leave out the cancer patients
2. Low Recall + High Precision — This just means the model is very picky. It doesn’t generate a lot of false positives but misses out on a lot of the real cancer patients. Such models cannot be used for life critical data e.g. cancer detection, terrorist identification, accident prevention etc.
3. High Recall+ Low Precision — The model is able to detect most of the positives well but ends up creating a lot of false alarms. Such models should not be used for cases where false alarms have a huge cost — e.g. flight landing systems, crowd management systems, war prediction systems etc. Note that such models can work for life critical situations. It is still better to classify a few healthy patients as cancer patients than vice versa.

Needless, to say that when both of these are low the model is pretty useless.

When do we use these metrics?

Costly false negatives

Let’s say we have breast cancer patients. We would not like to leave out even a single patient undetected. We can still afford to have some of the healthy ones detected for cancer. Further tests always reveal the true nature in such cases. But specifically for such scenarios we should look at both sensitivity and specificity and try to have a high sensitivity.

Costly false positives

On the other hand let’s say we have a judge deciding whether an accused should be punished or not. In this case we can’t afford false positives. The law says that “We can let 10 criminals go unpunished but we can’t convict an innocent person”. Such cases would warrant high specificity.

Irrelevant true negatives

Google shows us millions of results for a single search query. It cares a lot about true positives (i.e. the webpage that matches our query) but it allows some false positives as well (i.e. search results that are not relevant to our query). Google certainly doesn’t care about true negatives (the search results that it didn’t show and were irrelevant.

TL;DR

• Accuracy — percentage of correct predictions
• Precision — how relevant are the positives
• Recall — same as sensitivity
• Sensitivity — % of actual positives detected
• Specificity — how well can we avoid false alarms

X8 aims to organize and build a community for AI that not only is open source but also looks at the ethical and political aspects of it. We publish an article on such simplified AI concepts every Friday. If you liked this or have some feedback or follow-up questions please comment below.

Thanks for Reading!